統計學課本重點摘要

CH1統計學基本元素

Population, Sample, Experimental unit

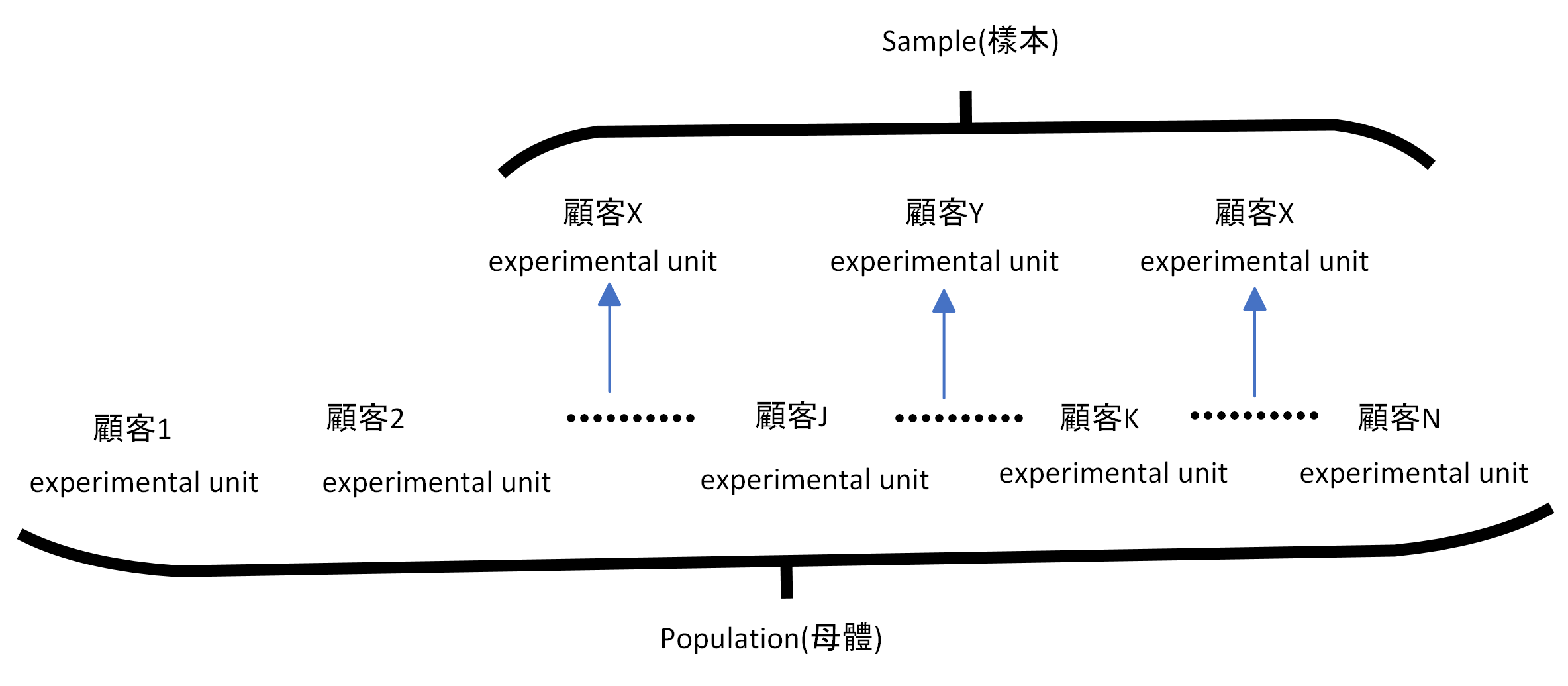
Variable

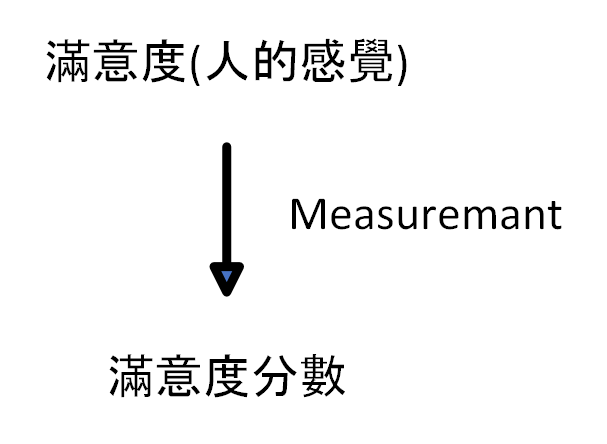
Measurement

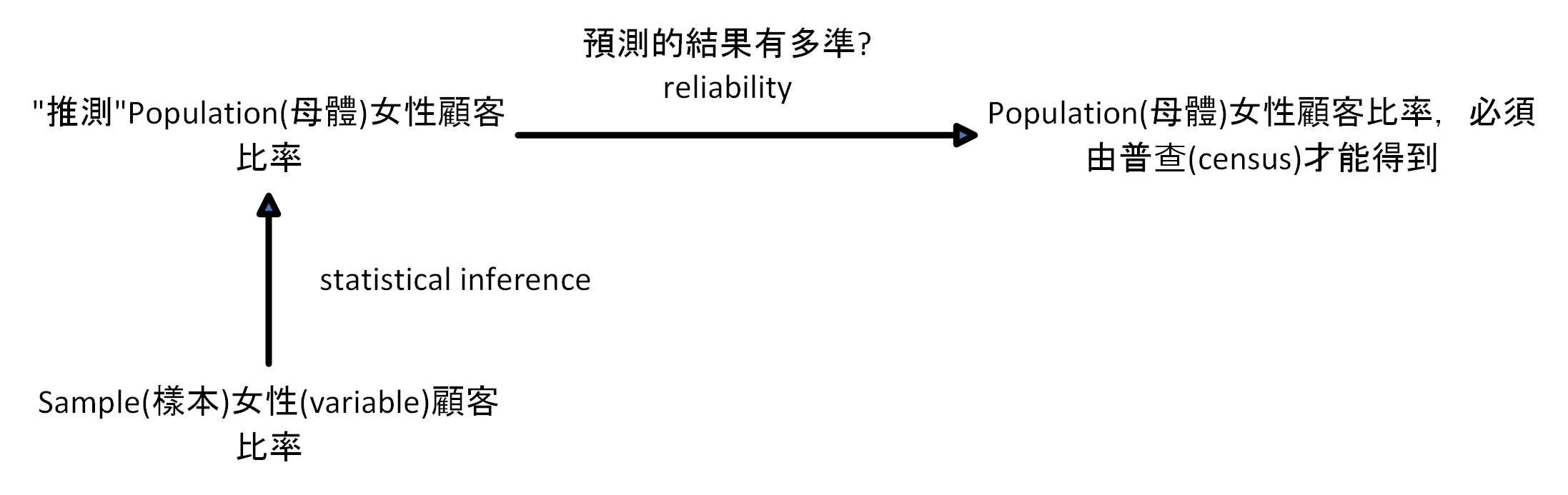
Inferenital Statistical Problem最大的重點，計算reliability

Quantitative data和Qualitative data

Quantitative data: 可以測量的資料，例如高度、溫度
Qualitative data:無法測量的資料，例如滿意度、車子種類，為了方便計算可以給予數值，但數值本身沒有任何意義，只是一個代號

Representative sample

representative sample的特遮會和母體的特徵一樣。

CH2 描述一組資料

資料集

data set: $$x_1, x_2, x_3, \cdots , x_n$$，每個元素都是一個量測結果。
例如我們量測5個商品的長度，並且記錄結果為$$x_1=5, x_2=3, x_3=8, x_4=5, x_5=4$$

加總符號

如果要表達所有元素的加總，我們可以寫成$$x_1 + x_2 + x_3 + \cdots + x_n$$，或是我們可以用符號
$$\sum$$代表

$$x_1 + x_2 + x_3 + \cdots + x_n = \sum_{i=1}^nx_i$$

如果我們要計算每個元素的平方和，可以表達成下面方式

$$x_1^2 + x_2^2 + x_3^2 + \cdots + x_n^2 = \sum_{i=1}^nx_i^2$$

描述資料的方式

通常描述資料會有兩中方式

1. 集中趨勢(central tendency)
2. 變異性(variability)
   (補集中趨勢和變異性的圖)

集中趨勢(Central Tendency)

1. 我們最常用的Central Tendency計算方式就是平均值，我們用$$\bar{x}$$(音:x bar)代表”樣本平均數”，他的計算方式如下

$$\bar{x} = \frac{\sum_{i=1}^nx_i}{n}$$

而我們用$$\mu$$代表母體平均數。通常我們用英文字母代表樣本，希臘字母代表母體。

2. 中位數，比起平均數更能夠對付極端值。

變異性(variability)

• deviation: 每一個資料點和平均的”距離”和”方向”，注意deviation是有正負號的，所以直接相加平均正負會相消。
• sample variance(變異數): 為了解決正負相消的問題，我們可以將每一個deviation平方後相加再除以元數個數-1。

$$s^2 = \frac{\sum_{i=1}^n(x_i - \bar{x})^2}{n-1}$$

• sample standard devitaion: 為了得到有意義的變異測量值，將sample variance開根號後就可以得到sample standard devitaion

$$s = \sqrt{s^2}$$

$$s^2 = $$ sample variance(樣本變異數)
$$s = $$ sample standard devitaion(樣本標準差)
$$\sigma^2 =$$ population variance(母體變異數)
$$\sigma =$$ population standard devitaion(母體標準差)

用標準差來描述單一樣本(單一資料集)

前面我們已經知道如果比較兩個樣本，standard devitaion越大表示變異性越大，也就是我們知道用standard devitaion來比較兩個樣本的相對變異程度。這節我們要用standard devitaion來描述單一個樣本。
如果對於frequency distributionj為對稱鐘形，根據經驗法則，

1. 通常68%的Experimental unit會落在平均的正負一個標準差之內，也就是對於樣本來說$$(\bar{x} - s, \bar{x} + s)$$，對於母體來說$$(\mu - \sigma, \mu + \sigma)$$
2. 通常95%的Experimental unit會落在平均的正負兩個標準差之內，也就是對於樣本來說$$(\bar{x} - 2s, \bar{x} + 2s)$$，對於母體來說$$(\mu - 2\sigma, \mu + 2\sigma)$$
3. 通常99.7%的Experimental unit會落在平均的正負三個標準差之內，也就是對於樣本來說$$(\bar{x} - 3s, \bar{x} + 3s)$$，對於母體來說$$(\mu - 3\sigma, \mu + 3\sigma)$$

描述單一個測量值在全部測量值的位置

如果要描述一個測量值在所有測量值的位置，例如個人所得在所有勞工所得的位置。我們可以用z-score來描述。z-score利用平均和標準差來描述一個側量值所在的位置。其公式如下。
對於樣本:

$$z = \frac{x - \bar{x}}{s}$$

對於母體:

$$z = \frac{x - \mu}{\sigma}$$

z-score是有正負號的，正值越大代表這個測量值大於平均值越多，反之越少。
(補上p79的圖)

CH3機率

事件、樣本空間、和機率

以丟硬幣為例

• observation, measurement:紀錄丟硬幣出現的結果
• experiment: 完成投擲多次硬幣並且記錄丟硬幣的結果的過程。
• sample point: 整個experiment最基礎的出現結果，以硬幣來說，正面反面各是一個sample point，以骰子來說1,2,3,4,5,6都分別是一個sample point。
  已丟兩個硬幣為例，總共有4個sample point，分別為正正、正反、反正、反反
• sample space:包含所有sample point的集合
  丟一個硬幣的sample space為 S:{正, 反}
  丟兩個硬幣的sample space為 S:{正正、正反、反正、反反}
  丟骰子的sample space為 S:{1,2,3,4,5,6}

sample point的機率規定

1. 每一個sample point的機率一定要介於0和1之間。
2. sample space裡面所有sample point的機率加總必須為1

event事件

event是一組sample point，他可以只包含一個sample point，也可以包含多個sample point

event的機率

就是event內所有的sample point的總和

聯集Unions和交集Intersections

聯集(or)
(P131的圖)
交集(and)
(P131的圖)

Complementary Event補集合

event A的補集合的事件就是由所有不包含A事件sample point所構成。$$A$$的補集合記為$$A^s$$

$$P(A)+P(A^s)=1$$

互斥事件的加法法則(Mutually Exclusive Events)

加法法則 $$P(A \cup B) = P(A) + P(B) - P(A \cap B)$$
互斥事件代表兩個事件不會同時發生，例如丟硬幣正面和反面不會同時出現，因此$$P(A \cap B)=0$$。因此對於互斥事件，$$P(A \cup B) = P(A) + P(B)$$

條件機率

給定A事件發生的條件下，B事件發生的機率。例如丟一個骰子，在丟出來的數字小於3的條件下，出現偶數的機率。

$$P(A \mid B) = \frac{P(A \cap B)}{P(B)}$$

乘法定律與獨立事件(Independent Event)

從前面的條件機率經過移項後就可以得到

$$P(A \cap B) = P(B)P(A \mid B)$$

而如果A和B的機率不會互相影響，A B兩個事件就是獨立事件，也就是

$$P(A \mid B) = P(A)$$

$$P(B \mid A) = P(B)$$
獨立事件有三個重點

1. 獨立事件沒辦法用作圖或是直覺判斷，必須透過計算來驗證他是獨立事件。
2. 互斥事件(Mutually Exclusive Events)不是獨立事件(Independent Event)，假設A，B為互斥事件，因為互斥事件的關係，如果B發生則$$P(A \mid B) = 0$$，而因此$$P(A) \neq P(A \mid B)$$，所以不可能滿足獨立事件的條件$$P(A \mid B) = P(A)$$。
3. 計算獨立事件的交集十分簡單，$$P(A \cap B) = P(A)P(B \mid A)$$，因為獨立事件的關係$$P(B \mid A)=P(B)$$，所以獨立事件的交集事件為$$P(A \cap B) = P(A)P(B)$$

隨機抽樣

每一個樣本被抽中的機率都相同

貝氏定律

$$P(A \mid B) = \frac{P(A \cap B)}{P(B)}$$
​

CH4隨機變數random variable和機率分布

隨機變數的兩種類型

• 隨機變數的定義
  隨機變數是把實驗會出現的所有結果用數字表達，每一個sample point都會有一個數字。例如以丟兩個銅板為例，我們可以計算出現人頭的數量，因此我們的random variable就會有0, 1, 2 三個。random在這裡代表的意義是這些數字在每次實驗中都是隨機出現的。

兩種類型的random variable

• discrete random variable 例如丟兩個銅板出現頭的個數
• continuous random variable 例如鑽油井挖到多深會挖到石油

probability distribution of diserete random variable

diserete random variable 的probability distribution可以是一個圖、表或是公式。他描述的是每一個random variable的發生的機率。
以丟兩個硬幣為例，我們以觀察到頭的個數作為random variable並計為x，x總共有三種可能，分別是頭出現0次，1次，2次(0, 1, 2)。
丟硬幣可能出現的sampling point共有HH, HT, TH, TT四種(H:頭, T:字)。
計算probability distribution如下

$$P(x=0)=P(TT) = \frac{1}{4}$$

$$P(x=1)=P(TH) + P(HT) = \frac{1}{2}$$

$$P(x=2)=P(HH) = \frac{1}{4}$$

probability distribution的必要條件

Discrete Random Variable x 的probability distribution必要條件

1. $$p(x) \geq 0$$
2. $$\sum{p(x)} = 1$$，其中 $$\sum{p(x)}$$ 是把所有可能的random variable x都算進去加總

期望值Expected Value

期望值其實就是population mean
以隨機變數Random Variable x為例
$$\mu = E(x) = \sum{xp(x)}$$
注意，期望值不一定會是Random Variable可能出現的值，以擲骰子為例，期望值不一定會是1~6其中一個整數

期望值的直觀解釋
https://www.probabilisticworld.com/intuitive-explanation-expected-value/

隨機變數的變異數(Variance)

$$\sigma^2 = E[(x - \mu)^2] = \sum{(x - \mu)^2p(x)}$$

隨機變數的標準差(Standard deviation)

$$\sigma = \sqrt{\sigma^2}$$

Sample Distributions

• parameters: 用來描述母體probability distributions的數值，例如用來描述binomial distributaion的成功機率p， 或者是描述normal distribution的$$\mu$$平均和$$\sigma$$標準差都是parameters。
  因為是描述母體，所以parameters是固定的數值，但是通常也是未知的或是永遠無法確切知道的

• sample statistic: 用來描述sample的數值，他是由sample的oberservation計算而來的。例如$$\bar{x}$$平均、$$s^2$$以及s標準差。
  藉由這些sample statistic內含的一些資訊，我們可以用來推斷母體的parameter。

sample statistic能夠直接拿來推論parameters嗎?

我們從由sample取得的一個oberservation可以算出sample statistic。每次的oberservation所計算的sample statistic也不完全相同。
舉例來說，我們想要推斷丟公平骰子出現點數的期望值$$\mu$$，而我們也已知$$\mu = 3.5$$(在現實情況下$$\mu$$幾乎都是未知的)。
假設每次oberservation都丟三次，第一次的觀察結果是2, 2, 6，$$\bar{x} = 3.33$$ 中位數m為3，我們可以看到$$\bar{x}$$比較接近母體的$$\mu$$。
第二次oberservation結果為3, 4, 6，$$\bar{x} = 4.33$$，m=4，這次反而是中位數比較接近母體的$$\mu$$。
由此可知我們沒辦法直接比較哪一個sample statistic比較適合拿來推論parameters，而其根本的原因是因為sample statistic本身也是random variable，因為不同的sample本身就會產生出不同的sample statistic。
也因為sample statistic是random variable的原因，要比較他們就必須用他們的probility distribution

sample statistic的sampling distribution

sample statistic的probility distribution稱為sampling distribution。舉例來說，假設一間工廠生產的鐵條長度$$\mu = 0.3$$標準差為0.005。假設一個實驗每次隨機抽出25根鐵條，並且量測每一根的長度後計算平均長度$$\bar{x}$$。假如這個實驗做很多次的話，每一次實驗的$$\bar{x}$$都會不太一樣，而這些大量實驗所產生的$$\bar{x}$$的分布圖就是$$\bar{x}$$的sampling distribution。
sampling distribution是經由重複操作”抽取n個measurements”的實驗所計算的sample statistic的分布

圖例:
https://onlinestatbook.com/stat_sim/sampling_dist/index.html

Sample Distribution形狀的特性

假如被抽樣的母體是常態分布，而且也只有母體是常態分布的情況下，則不管實驗抽樣的n的大小，他的Sample Distribution也一定是常態分佈

中央極限定理(Central Limit Theorem)

假設我們想要推論一個母體的平均數$$\bar{x}$$，於是我們進行抽樣並且每次實驗都抽取n個樣本來計算平均，這個實驗重複非常多次而得到Sample Distribution，我們可以觀察到$$\bar{x}$$的Sample Distribution的母體平均數$$\mu_\bar{x}$$、標準差$$\sigma_\bar{x}$$，以及被抽樣的母體的平均數$$\mu$$和標準差$$\sigma$$的關係為

1. Sample Distribution的平均 = 母體的平均，$$\mu_\bar{x} = E(\bar{x}) = \mu$$
2. $$Sample Distribution的標準差等於 = \frac{母體標準差}{\sqrt{n}}$$，也就是
   $$\sigma_\bar{x} = \frac{\sigma}{\sqrt{n}}$$
   不管母體的分布是什麼，當n月大的時候Sample Distribution就越接近常態分佈，而且並議會越小越，資料越集中。

CH5 Inference Based on a Single Sample

本章的重點在於如何運用一組資料(Single Sample)來進行預測

target parameter

對於母體我們有興趣但是未知的參數我們稱為target parameter例如母體平均數。

point estimator

利用樣本的一個數值來預測母體的target parameter稱為point estimator。例如我們利用樣本的平均$$\bar{x}$$來推估

母體平均的信賴區間 : Normal (z) Statistic

假設銀行要推估所有欠債兩個月以上的帳號平均欠債的金額，於是做了一次實驗抽出一百個欠債兩個月以上的帳號並計算樣本平均$$\bar{x}$$。接下來要計算樣本平均$$\bar{x}$$推估母體平均的準確度。
先回顧一下根據中央極限定理，樣本平均的Sample Distribution在每次抽樣的樣本數n夠大的時候會接近常態分佈。而interval estimator如下:
$$\bar{x} \pm 1.96\sigma_\bar{x}= \bar{x} \pm \frac{1.96\sigma}{\sqrt{n}}$$

從Sample Distribution得圖上來看，我們畫了一個上下邊界在Sample Distribution上，而邊界的中心是母體標準差。(根據中央極限定理，Sample Distribution的平均數會近似於母體平均數)。
回到我們計算欠債平均金額的實驗中，我們這次實驗取得的樣本會落在這上下邊界範圍內的機率是多少?因為如果我們取得的樣本可以落在這上下邊界之內，我們所算出來的interval estimator就會包含母體平均，超過邊界則interval estimator內不會包含母體平均。
從常態分佈下抽取一個樣本落在距離平均一個標準差內機率0.95。
可以參考下面網站

簡單來說，我們在這裡算出一個interval estimator，而真正的母體平均數會落在這個interval estimator內的機率是confidence coefficient。
{: .prompt-warning }

confidence level 和 confidence coefficient

confidence coefficient是我們隨機抽取的樣本所匯出的confidence interval包含母體平均的機率，而confidence level則是confidence coefficient以百分比的方式呈現。例如confidence coefficient為0.95，則confidence level為95%。

使用Normal (z) Statistic的條件

1. 樣本數n要大於30，因為根據中央極限定理當n大於30時，Sample Distribution會接近常態分佈。
2. 樣本必須是從母體中隨機抽取的

$$\alpha$$與confidence coefficient

利用樣本的一個數值來預測母體的target parameter稱為point estimator。例如我們利用樣本的平均$$\bar{x}$$來推估。
例如:
假設我們想要估計一個城市的平均收入，但我們無法調查每一個人。因此，我們可以從這個城市隨機抽取一些人（樣本），並計算他們的平均收入（樣本平均值）。然後，我們可以使用這個樣本平均值作為整個城市平均收入的點估計。

interval estimator

interval estimator是一個公式，它告訴我們如何使用樣本數據來計算一個區間，以估計目標參數。

Confidence Interval for a Population Mean: Normal (z) Statics

假設銀行想推估呆帳平均所欠下的金額，於是隨機抽樣100個呆帳帳戶出來計算出sample mean $$\bar{x}$$，並且想利用$$\bar{x}$$推估母體的平均$$\mu$$。在這裡$$\bar{x}$$就是$$\mu$$的point estimator。
接下來要計算interval estimator，而根據Central Limit Theorem可以知道如果每次抽樣的數量n夠大，則Sample Distribution接近為常態分布，而且Sample Distribution的平均值

如此一來我們可以改寫confidence interval的公式為:

$$\bar{x} \pm (z_{\frac{\alpha}{2}})\sigma_{\bar{x}}= \bar{x} \pm z_{\frac{\alpha}{2}}(\frac{\sigma}{\sqrt{n}})$$

其中$$z_{\frac{\alpha}{2}}$$為z值在頭部面積為$$\frac{\alpha}{2}$$的時候的值。
而$$\sigma_{\bar{x}}$$ 是sample statistic $$\bar{x}$$ 的Sample Distribution，計算方式是母體標準差除以樣本數的平方根。當樣本數夠大的時候(通常大於30)，可以用單次抽樣的標準差sample statistic s代替母體標準差$\sigma$。
也就是說當樣本數大於30時，式子可以改寫成
$$\bar{x} \pm (z_{\frac{\alpha}{2}})\frac{s}{\sqrt{n}}$$

概念釐清

特別注意，這個章節我們的目標是只做一次experiment，進而推斷出母體平均數。所以我們Sample Distribution是未知的，因為Sample Distribution要做很多次實驗才能得到。
這也就是為什麼$$\sigma_{\bar{x}}$$是未知的，而且$$\sigma_{\bar{x}}$$所指的母體是Sample Distribution，跟我們要推估的母體不是同一個母體。
{: .prompt-warning }

5.3 Student’s t Statistic

有些狀況下我們可以抽取的樣本數很少，例如藥物的人體實驗，這是後使用z statistic就會變得不準確。這裡將介紹t Statistic來處理這個狀況。
當樣本數小於30的時候我們面臨兩個問題

1. 樣本數小於30，不能使用中央極限定理，也因此不能直接假設Sample Distribution為常態分佈。
   • 解法:在前面我們可以發現到，如果母體為常態分佈，那即使樣本很少，Sample Distribution也會接近常態分佈。引此我們假設母體為常態分布。
2. 母體標準差$\sigma$是未知的而且我們不能再用單次抽樣的標準差s來代替，因為樣本數太少了。所以z statistic的公式也不能使用，因為他需要$\sigma$良好的估計值。
   • 解法:我們定義t statistic來處理這個問題。t statistic的公式如下
     $$t=\frac{\bar{x}-\mu}{s/\sqrt{n}}$$

在這裡sample statistic s是單次抽樣的標準差，取代了母體標準差$\sigma$。
假如我們是從常態分佈的母體抽樣，那麼t statistic的分佈會接近常態分佈。而t statistic和z statistic的差別在於t statistic多了一個random quantities s，也因此他的變動會比z statistic大。

t的Sample Distribution中實際變異量取決於樣本大小n。我們通常將他表示為自由度(degrees of freedom)為n-1的t分佈。回顧一下(n-1)是計算$s^2$的分母，所以如果n越小那sample distribution的變異量就越大。

對於small-sample 的confidence interval有以下結論

• 對於平均數$\mu$，small-sample的confidence interval如下，其中$t_{\frac{\alpha}{2}}$為(n-1)自由度

$\bar{x} \pm t_{\frac{\alpha}{2}}\frac{s}{\sqrt{n}}$

• 計算small-sample的confidence interval有以下條件
  • 樣本是隨機從母體抽出
  • 母體的分布必須接近常態分布

5.3 Large-Sample Confidence Interval for a Population Proportion

以市場調查為例，一間公司想知道消費者會選擇自己的品牌或是其他品牌。注意在這裡選擇品牌是一個qualitative variable，所以我們要用proportion來描述，而且這個問題是一個二元問題，因此我們要計算的是binoimal experiment中的p，也就是成功比例。要估計p我們可以利用計算樣本的成功比$\hat p$

$$\hat p=\frac{x}{n}=\frac{消費者選擇這間公司的品牌的人數}{問卷總人數}$$

而為了要計算$\hat p$的可靠度，我們將$\hat p$視為平均數，也就是說選擇這間公司品牌的人p計為1，選擇其他品牌的人q計為0，全部相加後除與總抽樣人數n，如此一來就可以用前面計算平均數的方法來推估$\hat p$的可靠度。

$\hat p$ 的Sampling Distribution

1. $\hat p$的Sampling Distribution的平均數為p
2. $\hat p$的Sampling Distribution的標準差為$\sqrt{\frac{pq}{n}}$，也就是$\sigma_{\hat p} = \sqrt{\frac{pq}{n}}$
3. 對於large samples，$\hat p$的Sampling Distribution接近常態分佈。large samples的定義為np>5且nq>5。

常用參考資料

https://cqeacademy.com/cqe-body-of-knowledge/quantitative-methods-tools/point-estimates-and-confidence-intervals/